Lineāru līdzstrāvas ķēžu aprēķinu metodes

Kirhofa likumu metode

1. Brīvi izvēlamies zaru strāvu virzienus.

2. Uzrakstām m-1 vienādojumus pēc mezglu punktiem, kur m ir mezglu punktu skaits attiecīgajā slegumā (skatīt 1.1. att.).

3. Izvēlamies neatkarīgos kontūrus k=z-(m-1), kur z- shēmas zaru skaits.

4. Tālāk mēs izvēlamies kontūra apiešanas virzienus un sastādam vienādojumus.

5. Atrsinam šīs vienādojumu sistēmas ar jebkuru lineāro vienādojumu sistēmu paņēmienu jeb metodi.

Risinājums:

1) visi mezglu punktu vienādojumi:

b=I2-I5-I1+I4=0

g=-I2+I3+I5-I6=0

d=-I3+I1-I4+I6=0

2) visi kontūru vienādojumi:

abg= I2*R2+I5*R5=E2

bcd= I1*R1+I4*R4=E1

dgb= -I5*R5 - I4*R4-I6*R6=0

defg= I3*R3+I6*R6=-E3

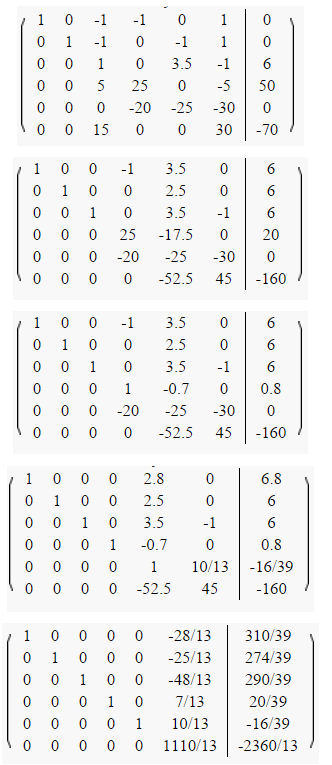
3) Tālāk, veicot aprēķinus, mēs iegūstam šādu matricu:

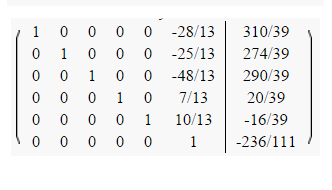
4) Šo matricu mēs atrisinām, izmantojot Gausa metodi:

5) Tālāk no iegūtā rezultāta mēs izteiksim strāvu stiprumus:

I1= 374/111=3,369 A

I2= 326/111=2,937 A

I3= -46/111= -0,414 A 

I4= 184/111=1,658 A

I5= 136/111=1,225 A

I6= -236/111= -2,126 A 

Mezglu potenciālu metode

1. Izvēlas mezglus, kuriem uzrakstīt vienādojumus, pieņemot viena mezgla potenciālu vienādu ar nulli!

2. Uzrakstot vienādojumu vienam no mezgliem, piemēram, g mezglam, vienādojumu kreisajā pusē ar plusa zīmi raksta šī mezgla potenciālu Φg, kas reizināts ar mezglam g tieši pieslēgto vadītspēju summu.

3. Ar mīnusa zīmi vienādojuma kreisajā pusē raksta pārējo mezglu potenciālus, kas reizināti ar to zaru vadītspēju summu, kuri tieši savieno šos mezglus ar mezglu g, (potenciālus mezgliem, kuri nav tieši savienoti ar mezglu g, mezgla g vienādojums nesatur).

4. Vienādojuma labajā pusē raksta mezglam g tieši pieslēgto strāvas avotu strāvu algebrisko summu. Ar plusa zīmi raksta uz mezglu g vērsto strāvas avotu vērtības, bet ar mīnusu prom vērstās strāvas avotu vērtības.

5. Vienādojuma labajā pusē raksta g mezglam tieši pieslēgto zaru EDS un šo zaru vadītspēju G reizinājumu algebrisku summu. Summas locekļus raksta ar plusa zīmi, ja EDS avots ir vērsts uz mezglu g, ja EDS avots ir vērsts prom no šī mezgla, tad to raksta ar mīnusa zīmi.

6. Pēc iegūtās vienādojumu sistēmas atrisināšanas atrod zaru strāvas, izmantojot Kirhofa otro likumu, kas uzrakstīts atsevišķiem zariem (vispārināts Oma likums).

Risinājums:

1) Vienādojumi:

Φd = 0 V

b = Φb*(G1+G2+G4+G5) - Φg*(G5+G2)= E2*G2-E1*G1

g = Φg*(G2+G3+G5+G6) - Φb*(G5+G2)= -E2*G2-E3*G3,

kur G- vadītspēja.

2) Tālāk mēs aprēķināsim atsevišķās vadītspējas:

G1 = 1/5 = 0,200 S

G2 = 1/10 = 0,100 S

G3 = 1/15 = 0,067 S

G4 = 1/20 =0,050 S

G5 = 1/25 =0,040 S

G6 = 1/30 = 0,033 S

3) Tālāk mēs iegūtās vērtības ievietosim vienādojumā:

Φb*(0,2+0,1+0,05+0,04) – Φg*0,14 = 60*0,1-50*0,2

Φg*(0,1+0,067+0,04+0,033) - Φb*0,14 = -60*0,1-70*0,067

Φb*0,39- Φg*0,14 = -4 

Φg*0,24- Φb*0,14 = -10,69

4) Tālāk vienādosim vienu no nezināmajiem, lai vēlāk varētu to atmest!

(Φb*0,39- Φg*0,14 = -4)*1,714 (papildreizinātājs 1,714)

-Φb*0,14+Φg*0,24 = -10,69

5) Tālāk mēs iegūstam, ka:

Φb*0,66846- Φg*0,24= -6,856 (vērtības atņemsies, paliks tikai Φb)

-Φb*0,14+Φg*0,24= -10,69

6) Tālāk mēs iegūstam, ka:

Φb0,52846= -17,546

Φb=-17,546/0,52846= -33,202 V

7) Tālāk ar ievietošanas paņēmienu mēs iegūsim otru nezināmo:

33,202*0,14+Φg*0,24= -10,69

Φg*0,24= -10,69-4,648

Φg= -15,338/0.24

Φg= -63,908 V

8) Tālāk mēs aprēķināsim strāvas, izmantojot sprieguma potenciālus:

I1= (Φb- Φd+E1)/R1=(-33,202-0+50)/5=3,359 A (atšķirība aiz komata ir novērojama, jo tika noapaļots skaitlis) 

I2= (Φg- Φb+E2)/R2=(-63,908-(-33,202)+60)/10=2,929 A (atšķirība aiz komata ir novērojama, jo tika noapaļots skaitlis)

I3= (Φg- Φd+E3)/R3=(-63,908-0+70)/15=0,406 A (atšķirība aiz komata ir novērojama, jo tika noapaļots skaitlis)

I4= (Φd- Φb)/R4=(0-(-33,202))/20=1,66 A (atšķirība aiz komata ir novērojama, jo tika noapaļots skaitlis)

I5=(Φb- Φg)/R5=(-33,202-(-63,908))/25=1,228 A (atšķirība aiz komata ir novērojama, jo tika noapaļots skaitlis)

I6=(Φd- Φg)/R6=(0-(-63,908))/30=2,13 A

*Atšķirība aiz komata ir novērojama, jo tika noapaļots skaitlis!

Kontūrstrāvu metode

1. Ir jāizvēlas neatkarīgos kontūrus (t.i., kontūrus, kuriem būtu jāsastāda vienādojumi pēc Kirhofa otrā likuma, zari ar strāvas avotiem, kā zināms, šos kontūrus neveido).

2. Izvēlas papildus kontūrus tā, lai caur katru strāvas avotu ietu vienīgais papildus kontūrs un tā kontūrstrāvas virziens sakristu ar strāvas avota virzienu. Ārpus strāvas avotiem šos papildu kontūrus var noslēgt pa jebkuru ceļu (vēlams - pa īsāko).

3. Uzraksta vienādojumus tikai neatkarīgajiem kontūriem, taču ievērojot arī papildus kontūrstrāvu izraisītos spriegumus. Rakstot i-kontūra vienādojumu, tā kreisajā pusē raksta kontūrstrāvu Iik, reizinātu ar i-kontūra visu pretestību summu, un citas kontūrstrāvas, piemēram, Ijk, kuras plūst i- un j-kontūra kopīgajos zaros, reizināts ar abu kontūru kopīgo zaru pretestību algebrisko summu. Kontūrstrāvas Ijk un kopīgā zara pretestības reizinājums šajā summā rakstāms ar plusa zīmi, ja abu kontūrstrāvu virzieni šajā pretestībā sakrīt, bet ar mīnusa zīmi, ja tie ir pretēji viens otram. Kontūrstrāvas, kuru kontūriem nav kopīgu zaru ar i-kontūru, šajā kontūra vienādojumā neparādās.

4. Vienādojuma labajā pusē, ja strāvas avotu ietekme ir ievērota ar papildu kontūrstrāvu palīdzību, raksta tikai attiecīgā kontūra EDS algebrisku summu kā Kirhofa otrā likuma vienādojumā, par apejas virzienu uzskatot kontūrstrāvas virzienu. Tā iegūst k vienādojumu sistēmu ar tikpat nezināmajām kontūrstrāvām.

5. Pēc vienādojumu sistēmas atrisināšanas zaru strāvas atrod kā to kontūrstrāvu algebriskas summas, kuras plūst apskatāmajā zarā, ievērojot arī papildu kontūrstrāvas. Ar plusa zīmi rakstāmas tās kontūrstrāvas, kuru virziens apskatāmajā zarā sakrīt ar pieņemto zara strāvas virzienu, bet tās, kuras vērstas pretēji šim virzienam, rakstāmas ar mīnusa zīmi.

Risinājums:

1) Vienādojumi:

bcd: Ik3*(R1+R4) - Ik2*R4=E1

dgb: Ik2*(R6+R5+R4) - Ik3*R4- Ik4*R6- Ik1*R5=0

defg: Ik4*(R3+R6) - Ik2*R6=-E3

abg: Ik1*(R2+R5) - Ik2*R5=E2

2) Tālāk šos vienādojumus ievietosim sistemā, kuru atrsinās, izmantojot Krāmera formulu:

0*Ik1-20*Ik2+ 25*Ik3+0*Ik4= 50 V

-25*Ik1+75*Ik2 - 20*Ik3 - 30*Ik4= 0 V

0*Ik1-30*Ik2+0*Ik3+45*Ik4= -70 V

35*Ik1-25*Ik2+0*Ik3+0*Ik4= 60 V

3) Tālāk mēs iegūstam:

,

kur x1, x2, x3, x4 – kontūrstrāvas atbilstoši to piešķirtajiem numuriem, kur x1 ir Ik1, x2 ir Ik2 utt.

4) Tālāk mēs aprēķināsim atsevišķās strāvas:

I1=Ik3=374/111= 3,369 A

I2=Ik1=326/111= 2,937 A

I3=-Ik4=-(-46/111)= 0,414 A

I4=Ik3-Ik2=3,369-1,712= 1,657 A

I5=Ik1-Ik2=2,936-1,712= 1,224 A

I6=Ik2-Ik4=1,712-(-0.414)= 2,126 A

Visu trīs metožu salīdzinājums

Ja salīdzina trīs dažādas lineāru līdzstrāvas ķēžu metodes, tad mēs nonākam pie secinājuma, ka visas trīs aprēķinu metodes ir ekvivalentas, tās var izmantot vienkāršu līdzstrāvas ķēžu aprēķinos, tās var aizstāt vienu ar otru, lai pēc iespējas ātrāk un precīzāk atrastu nepieciešamos strāvu stiprumus ķēdēs. Visu trīs metožu salīdzinājumus skatīt 1.1 tabulā.

1.1 tabula

Strāva, A Metode	I1, A	I2, A	I3, A	I4, A	I5, A	I6, A
Kirhofa likumu metode	3,369	2,937	0,414	1,658	1,225	2,126
Mezglu potenciālu metode	3,359	2,929	0,406	1,660	1,228	2,130
Kontūrstrāvu metode	3,369	2,937	0,414	1,657	1,224	2,126